המתמטיקה מוגדרת לעיתים קרובות כלמידת הדפוסים והתבניות של מבנה, שינוי ומרחב, ואפיונם. מנקודת מבט מודרנית, מתמטיקה היא השימוש בלוגיקה פורמלית לחקירת מערכות ומבנים מופשטים שהוגדרו אקסיומטית.
מוצאם של רוב המבנים הנחקרים במתמטיקה הוא ממדעי הטבע, לרוב מפיזיקה, אך מתמטיקאים מרבים להגדיר ולחקור מבנים מסיבות פנימיות לחלוטין למתמטיקה עצמה, למשל לשם ביצוע הכללה מאחדת של תחומים מתמטיים אחדים או ככלי שימושי לביצוע חישובים. יש אפוא מתמטיקאים רבים שחוקרים תחומים מסוימים מסיבות אסתטיות לחלוטין, בראיית המתמטיקה כאמנות במידת מה יותר מכמדע שימושי.
|
|
חזקה היא פעולה מתמטית המתבצעת בין שני מספרים ומסומנת . בצורתה הבסיסית ביותר, כאשר הוא מספר טבעי, החזקה שווה ל- מופעים של הנכפלים זה בזה. את ההגדרה הבסיסית הזו ניתן להרחיב למערכות מספרים רבות, ואף לעצמים מתמטיים שאינם בהכרח מספרים, תוך שמירה על תכונותיה הבסיסיות הייחודיות של הפעולה, הנקראות חוקי חזקות.
לחזקה תפקיד מרכזי בתחומים רבים במתמטיקה. השערות ומשפטים הקשורים בפעולה העסיקו מתמטיקאים במשך מאות שנים. פונקציות המבוססות על פעולת החזקה, כגון פולינומים ופונקציות מעריכיות, משמשות בכל תחומי המדעים. בשל כך פותחו שיטות המאפשרות חישוב חזקות באופן יעיל, במקום הכפלה חוזרת שעשויה לקחת זמן רב.

סר אייזק ניוטון (באנגלית: Isaac Newton; 4 בינואר 1643 – 31 במרץ 1727 היה פיזיקאי, מתמטיקאי, אסטרונום, פילוסוף ואלכימאי אנגלי, הנחשב לאחד מגדולי המוחות המדעיים בכל הזמנים.
חיבורו "היסודות המתמטיים של פילוסופיית הטבע" שפורסם ב-1687 הכיל תיאור של כוח הכבידה ושלושת חוקי התנועה, והניח את הבסיס למכניקה הקלאסית ששלטה בראייה המדעית של היקום הפיזיקלי במשך שלוש המאות הבאות ויצרה את הבסיס להנדסה המודרנית.
ניוטון נחשב לאבי החשבון הדיפרנציאלי והאינטגרלי, הציג לראשונה את משפט הבינום המוכלל (אשר נקרא על שמו – הבינום של ניוטון), המתאר את טור טיילור של הפונקציה גם כאשר אינו שלם, הוא פיתח והציג את זהויות ניוטון, שיטת ניוטון-רפסון למציאה נומרית של שורשי פונקציה, התורה של פולינומים ממעלה שלישית בשני משתנים, תרם תרומות חשובות לתורה של הפרשים סופיים והיה הראשון שהשתמש באינדקסים חלקיים ובגאומטרית קוארדינטות כדי לגזור פתרונות למשוואה דיופנטית. ניוטון החל גם לפתח את חשבון הווריאציות, תחום שקיבל שם זה רק במאה ה-18. כמו כן גילה נוסחה חדשה לחישוב π.

הטסרקט, שהוא גוף ארבע ממדי המהווה הכללה של הקובייה, כפי שהוא נראה לאחר הטלה סטריאוגרפית מן ה-3-ספירה אל המרחב האוקלידי התלת־ממדי, בעיניה של ג'ני.


הכרך האחרון מבין שלושה עשר כרכי חיבורו החשוב של אוקלידס, יסודות, עסק בחמשת הפאונים המשוכללים, והופיעה בו הוכחה לכך שהם הפאונים המשוכללים היחידים. אפלטון קישר בין היותם של חמישה גופים כאלו לחמשת יסודות הטבע בעיניו- ארבעון לאש, קובייה לאדמה, תמניון לאוויר, עשרימון למים ואת התריסרון בן שתים עשרה הפאות לגלגל המזלות. קישור שכזה בין העולם המתמטי לטבע יכול להיראות מופרך לקורא המודרני, אך גם ב-1596 האסטרונום יוהאנס קפלר פרסם חיבור בו טען שמסלוליהם של ששת כוכבי הלכת שהיו ידועים בזמנו הם למעשה כדורים, החוסמים ונחסמים באחד מהגופים האפלטוניים, כלומר ברווחים שבין המסילות של כוכבי הלכת לשמש ניתן להכניס בדיוק את אחד הגופים המשוכללים.
כל פעילות אנושית, טובה או רעה, להוציא מתמטיקה, חייבת להגיע לכלל סיום
נוסחה להפרש של שני ריבועים. נוסחה בסיסית באלגברה. כמו יתר הנוסחאות באלגברה בסיסית, פיתוח הנוסחה פשוט מאוד ומבוסס על חוק הפילוג, חוק הקיבוץ וחוק החילוף. אולם שימוש בנוסחה "לכיוון השני" מימין לשמאל מאפשר לבצע מניפולציות לא טריוויאליות משום שהוא מחליף ביטוי שעל פניו לא נראה פריק, במכפלה של שני ביטויים פשוטים יותר. על נוסחה זו מבוסס טריק שנקרא מכפלה בצמוד
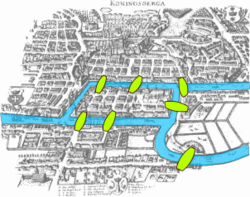
בתמונה מופיעה מפה של הגשרים של קניגסברג. האם יש מסלול סגור העובר דרך כל אחד מהגשרים פעם אחת בלבד? אם כן, מהו?
| פתרון | |
|---|---|
|

בחלון זה מופיעה תצוגה מתחלפת של אתרי אינטרנט הפועלים להנגשת המתמטיקה לציבור הרחב.
אתר היום: MegaMath (באנגלית)
MegaMath הוא אתר המביא לתלמידי בית הספר היסודי את הרעיונות והבעיות של המתמטיקה המודרנית: לוגיקה, האינסוף, תורת הגרפים, ועוד. זהו אתר חובה לשונאי מתמטיקה: אלה שמעולם לא הבינו דבר בתחום זה, אך פתוחים להזדמנות לגלות את יופיו. את האתר העניקה לעולם המעבדה הלאומית לוס אלמוס, המוכרת יותר בתרומתה לפיתוח נשק גרעיני.
בחלון זה מופיעה תצוגה מתחלפת של ספרי מתמטיקה שנועדו להנגשת המתמטיקה לציבור הרחב.
ספר היום:

רומה פלק, אתגרים לתאים האפורים – בעיות, חידות ולקחיהן, ספרית פועלים – הוצאת הקיבוץ המאוחד, 2004
הספר מכיל 122 חידות מתמטיות, מהן נודעות ומהן מקוריות. לכל חידה אתגר משלה, ולמי שלא הצליח לפצחו, ניתן פתרון מפורט. המחברת, רומה פלק מהאוניברסיטה העברית בירושלים, מנחה את הקורא:
- "איך לקרוא את הספר? לאט לאט ובמינון סביר. אני ממליצה להתייחס לספר זה כמו לשתיית קפה: לא יותר מדי בבת אחת ולא לפני השינה. מומלץ לחשוב לבד על כל בעיה לפני שמציצים בפתרונה. הפתרון יהיה הרבה יותר משמעותי בעבורכם אם הגעתם אליו (או לפתרון אחר) בכוחות עצמכם, או אף אם עשיתם חלק מהדרך ועמדתם על סוד הקושי והסיבוך של הבעיה."
|
משפטים מפורסמים
|
השערות מפורסמות
|
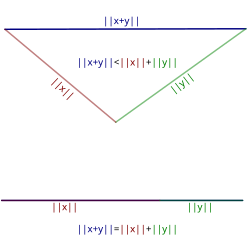
אי שוויון המשולש הוא התרגום האלגברי לעובדה שבמשולש, אורכה של כל צלע קטן מסכום ארכי הצלעות האחרות. אי-שוויון המשולש מבטא את העובדה שלא ניתן לקצר את הדרך מ- A ל- C על ידי מעבר בנקודה B (כלומר: הקו הישר הוא הדרך הקצרה ביותר בין שתי נקודות). בצורתו הפשוטה, עבור זוג מספרים ו- , מתקיים .
זוהי תכונה יסודית כל-כך של מושג ה"מרחק", עד שהיא מהווה אחת מהאקסיומות המגדירות מטריקה ומרחב מטרי. לפיכך, אי שוויון זה נכון, בהכללה, עבור כל נורמה (המושג "נורמה" הוא הכללה של מושג ה"אורך"). בפרט, אי שוויון המשולש האינטגרלי הוא גרסה של אי שוויון המשולש עבור הנורמה האינטגרלית.
| כמות | אינסוף - מספרים (טבעיים, שלמים, רציונליים, אי-רציונליים, ממשיים, מרוכבים) - מספרים סודרים - עוצמה - תורת המידה - קבועים מתמטיים | ||
|---|---|---|---|
| שינוי | אנליזה מתמטית - אנליזה וקטורית - אנליזה מרוכבת - אריתמטיקה - חשבון אינפיניטסימלי - תורת הכאוס - משוואות דיפרנציאליות - אנליזה פונקציונלית | ||
| מבנה | אלגברה - אנליזה מתמטית - אריתמטיקה - טופולוגיה - תורת הגרפים - תורת החבורות - תורת המספרים | ||
| מרחב | אלגברה ליניארית - גאומטריה - טופולוגיה - טריגונומטריה - אנליזה וקטורית - חשבון טנזורים - מרחב מחויג | ||
| מתמטיקה בדידה | חישוביות - קומבינטוריקה - קריפטוגרפיה - תורת הגרפים - תורת המשחקים | ||
| יסודות ושיטות | לוגיקה - פילוסופיה של המתמטיקה - תורת הקבוצות - סימון מתמטי - תורת הקטגוריות | ||
| מתמטיקה יישומית | אופטימיזציה - אנליזה נומרית - הסתברות - סטטיסטיקה - מתמטיקה פיננסית | ||
| עולם המתמטיקה | הוראת המתמטיקה - האיחוד המתמטי הבינלאומי - היסטוריה של המתמטיקה - מדליית פילדס - מתמטיקאים - 23 הבעיות של הילברט | ||
לוגיקה מתמטית הוא תחום במתמטיקה, העוסק במערכות פורמליות ובדרך בה הן מקודדות מושגים אינטואיטיביים, כגון הוכחה או חישוביות. במקורה הייתה הלוגיקה ענף של הפילוסופיה, אולם במהלך מאתיים השנים האחרונות חלו התפתחויות רבות בתחום הלוגיקה הפורמלית שהינה כיום, בנוסף לפילוסופיה, גם ענף של המתמטיקה הנקרא לוגיקה מתמטית.
התחום הוא אחד מקבוצה של תחומים המכונים יסודות המתמטיקה משום שהם עוסקים בבסיס הפורמלי של המתמטיקה כולה. לוגיקה מתמטית עוסקת באותם חלקים של הלוגיקה שניתן ליצור להם מודל מתמטי. בעבר נקרא התחום גם בשמות לוגיקה סימבולית (בשל עיסוקו בטענות המיוצגות בידי סמלים) או מטה-מתמטיקה. השם השני מתייחס כיום רק לתורת ההוכחות, אחד התחומים בלוגיקה מתמטית.
|
ערכים המחפשים עורכים  |
דיונים, ייעוץ ועזרה
|